样本量过少回归分析如何分析处理与解释
2017-03-21 刘重杰 刘重杰
回归是统计学中最常用的模型,但是,有时使用回归后发现结果难以解释,或者与临床实际并不符合,十分困惑。这可能是什么原因呢? 虽然,实际原因很多,但是重要原因之一是样本量太小!很小小样本得出回归的结果,其实并不"回 归",因此,在处理小样本做多因素回归分析时,要慎重。传统一般认为在logistic回归时,变量与样本量之比为至少5倍,即纳入5个变量时,样本量至少也需要25例,实际上,这是保守估计。如果
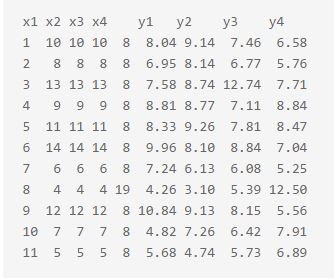
回归是统计学中最常用的模型,但是,有时使用回归后发现结果难以解释,或者与临床实际并不符合,十分困惑。这可能是什么原因呢? 虽然,实际原因很多,但是重要原因之一是样本量太小!很小小样本得出回归的结果,其实并不"回 归",因此,在处理小样本做多因素回归分析时,要慎重。传统一般认为在logistic回归时,变量与样本量之比为至少5倍,即纳入5个变量时,样本量至少也需要25例,实际上,这是保守估计。如果每个变量能超过40例样本时,回归的结果往往是不错的。 谈到回归,要讲其核心---最小二乘法(OLS)。 学会OLS,有人还明白了ML等方法的含义;现在学统计分析的时候,或多或少会安排统计软件的实践课程,于是大家学会了使用Excel,乃至SAS中如何来做经典的回归分析。看过不少的文献,很多都忽略了回归分析模型诊断这个环节——可能很多标准教科书没有强调,甚至是没有讲;这不能不说是一个遗憾。 回归分析使用最广泛,误用的情况也多了些。下面使用一个经典的例子,来“恶心”一下那些“过分钟爱”经典回归分析的人——我在很多课堂上都举过这个例子(Anscombe),作为从基础课程向中级乃至高级课程的开场白。上面有
作者:刘重杰
版权声明:
本网站所有注明“来源:梅斯医学”或“来源:MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明“来源:梅斯医学”。其它来源的文章系转载文章,本网所有转载文章系出于传递更多信息之目的,转载内容不代表本站立场。不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。
在此留言







想学习一下,这个太需要了
72
数完对点是什么意思
114
#样本#
68
学习了,非常感谢!
184
这个板块太好了,对学习非常有用。
136