正常值范围的估计的统计学测量
2018-07-13 MedSci MedSci原创
在医学科研中有时需要根据样本数据推论总体中个体值范围,其中最常用的是估计正常值范围。一、正常值范围的意义正常人体的解剖、生理、生化、心理等各种数据的波动范围称正常值范围,简称正常值。如成人白细胞总数的正常值为4000~10000个/mm3。以一定数量“正常人”为样本,观察某个或几个变量,根据所得样本数据,推论总体中变量值的范围,称正常值范围估计。一些与人体有关的外界环境如噪音强度、粉尘浓度、昆
在医学科研中有时需要根据样本数据推论总体中个体值范围,其中最常用的是估计正常值范围。
一、正常值范围的意义
正常人体的解剖、生理、生化、心理等各种数据的波动范围称正常值范围,简称正常值。如成人白细胞总数的正常值为4000~10000个/mm3。以一定数量“正常人”为样本,观察某个或几个变量,根据所得样本数据,推论总体中变量值的范围,称正常值范围估计。一些与人体有关的外界环境如噪音强度、粉尘浓度、昆虫密度、水中微量元素的含量等,在某一地域、某段时期内亦在一定范围内波动;某病患者在病程的某段时期内,某种检验结果亦常在一定范围内波动。虽然这些范围不一定是正常的,有的超过了卫生标准或正常值,但若从样本数据估计总体中变量值的范围来说,那么也可以用本章的估计方法,得出的波动范围可称为个体值范围。
二、确定正常值范围的一般原则和步骤
1.确定研究总体。即对研究总体的同质性基础作出规定。以“正常人”为例,所谓正常人不是指任何组织与器官的形态及机能都无异常的人,而是指排除了影响被研究指标的疾病和有关因素的人。例如某单位研究血清谷一丙转氨酶活性的正常值,选取“正常人”的条件为无肝、肾、心、脑、肌肉等器质性疾患,近期无特殊用药史(如氯丙嗪、异烟肼等),测定前未作剧烈运动等。上述条件就是保证研究对象的同质性作出的规定。但不允许以所研究指标值的大小来划分是否“正常人”。对研究总体,如“正常人”的规定要根据研究目的、技术力量与水平以及人力物力等条件来考虑,往往牵涉到多方面的专业知识。但一般可从地区、民族、性别、年龄、劳动条件(如是否与有害物质接触)、时间(季节与昼夜)、月经、妊娠、饮食、药物、生活习惯等来考虑。例如红细胞数及血红蛋白量,高原居民与平原不同,男子各异;人体血清胆固醇含量随年龄的增长而增加,妊娠期高于非妊娠期,冬季高于夏季,且受饮食影响;服用某些药物可直接增加检测的有关成分或干扰检测结果的准确性。
各种影响因素,有些可通过询问与体检严格控制,如排除那些与被研究指标有关的各病患者,或处于妊娠、经期的妇女,近期内服用某种药物者等;有些可用对调查资料分组统计的办法加以控制或研究。如先按男、女分别统计,然后检验两组数据的分布、均数与标准差等,有无差别,若有差别则分别求正常值,否则可合并求通用的正常值。
2.确定观察例数。正常值范围的影响因素复杂,要使样本分布能正确估计总体分布,例数不能太少,一般认为应在200例左右。数据变异不大,观测比较精确的,例数可相应少些;影响因素复杂、数据变异大,观测方法不够稳定的,例数相应要多一些。但要防止片面追求数量,而抽选样本不按规定,观测方法不统一,粗率马虎,以致影响原始数据的可靠性。
3.统一测定方法,控制实验误差,保证数据的可靠性。为达到上述要求应注意对检测人员(医生、检验人员等)的培训,以统一认识、统一方法和操作,标准化仪器和试剂,建立质量控制防止记录差错等。但也要尽量与应用正常值范围时的实际情况相一致,例如临床检验每一个标本只作一次,那么为确定正常值的检验每个标本亦只作一次,不能作两个平行样本求平均数后再估计正常值。否则可能定出的正常值范围较窄。
4.确定取单侧还是双侧界值。某些指标如白细胞总数,无论过低或过高都不正常,因此需要确定下限和上限两个界值,称双侧界值。有的指标如肺活量一般只认为过低是不正常,所以只需定下测界值,即下限;但血铅只是过高不正常,只需定上限。只需定下限或上限的,称单侧界值。确定取单侧还是双侧界值,应根据业务知识与指标用途。
5.确定适当的百分范围。调查一定数量的正常人若以某指标的最小、最大值作为正常值范围,常因调查例数的增加等遇到少数极端值,使正常值范围不稳定。因此统计上常采用一些方法,删去一定比例的极端值,使得出的正常值能较稳定地反映绝大多数正常人该指标的数值。那么绝大多数是指正常人的百分之多少呢?一般包括正常人的80%、90%、95%或99%等。这样,若按单侧计算,相应地将有20%、10%、5%或1%的正常人该指标值在正常值范围以外;若按双侧计算,相应地,过高、过低者各有10%、5%、2.5%或0.5%。这些指标值在正常值范围以外的正常人,将被错判为不正常。将正常错判为不正常,称为I型错误,或假阳性,其假阳性率或误诊率用α表示。但亦有些病人的指标值,可能落在正常值范围以内,这时就会将病人错判为正常人,这种错判Ⅱ型错误,或假阴性,假阴性率即漏诊率用β表示。确定合适的百分范围应根据研究目的,结合正常人和病人的数值分布,同时考虑α及β,一般有下列两种情况:
(1)正常人和病人的数据分布无重叠(见图5.4a)。这时只考虑减少α;
(2)正常人和病人的数据分布有重叠(见图5.4b)。这时两分布重叠部分内既有病人亦有正常人,若欲减少α,界值向右移,那么β将加大;若欲减少β,界值向左移,那么α将加大。通常兼顾α及β,取两曲线交点的横座标为界值,这时α与β之和为最小。但实用时还要考虑该正常值范围的主要用途,若用以普查初筛病人,则要减少假阴性,取80%或90%正常值范围;若用以确诊病人,则要避免假阳性,以取95%或99%正常值范围为宜。
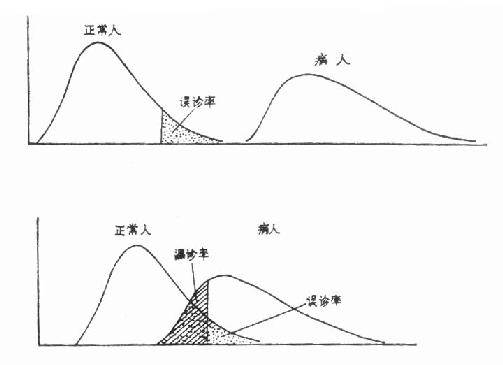
图 5.4 正常人和病人数据分布示意图
6.确定估计方法进行估计。估计正常值范围的方法较多,主要根据频数的分布类型和样本含量选用。常用的有百分位数法和正态分布法。运用百分位数法的条件是样本含量大,适用正态分布法的条件是资料服从正态分布或经过转换后服从正态分布。此外尚有曲线拟合法等。
三、确定正常值范围的方法
1.百分位数法。本法根据正常人样本数据,按照选定的百分范围计算相应的百分位数作为正常值范围的界值。可根据原始数据直接计算,亦可根据频数表进行计算。计算步骤为:
(1)按已确定的百分范围从表5.1查得应计算的百分位数;
(2)计算出各百分位数的所在位置;
(3)代入公式计算界限Px
表5.1 估计正常值范围的计算项目
| 百分范围(%) | 百分位数法 | 正态分布法 | ||
| 双侧 | 单侧 下(或上)限 | 双侧 | 单侧 下(或上)限 | |
| 80 | P10及P90 | P20(或P80) | X±1.282S | X-(或+)0.842S |
| 90 | P5及P95 | P10(或P90) | X±1.645S | X-(或+)1.282S |
| 95 | P 2.5及P97.5 | P5(或P95) | X±1.960S | X-(或+)1.645S |
| 98 | P1及P99 | P2(或P98) | X±2.326S | X-(或+)2.054S |
| 99 | P0.5及P99.5 | P1(或P99) | X±2.576S | X-(或+)2.326S |
例5.2 某地测得200例健康成人的血铅值(微克/100克)得频数分布如下,试估计单侧95%上限。
(1)查表5.1,百分范围95,百分位数法,单侧上限应求P95。
(2)求P95的位置200×0.95=190即为第190个数据处,因此知A=188,Lx=35,fx=4,ix=5。
代入公式(4.5)
表5.2 百分位数法计算单侧上限(200例健康成人的血铅值)
| 血铅值(微克/100克) | 频数 | 累计频数 |
| 0- | 6 | 6 |
| 5- | 48 | 54 |
| 10- | 43 | 97 |
| 15- | 36 | 133 |
| 20- | 28 | 161 |
| 25- | 13 | 174 |
| 30- | 14 | 188 |
| 35- | 4 | 192 |
| 40- | 4 | 196 |
| 45- | 1 | 197 |
| 50- | 2 | 199 |
| 55- | 0 | 199 |
| 60- | 1 | 200 |
| 合计 | 200 | - |
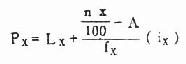
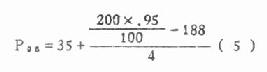
健康成人血铅值的95%正常值上限为37.5微克/100克。
若根据原始资料计算,已算得Px的位置为第190个数据后,将原始数据从大至小排,第10个数据的值即为Px。
此法的优点是不拘资料的分布类型,计算简便,样本含量较大,分布较稳定时结果稳定。但估计结果受样本极差的限制,受两侧尾部数据的影响较大,尤其是百分范围较大(如大于95%)。样本含量不够在时,结果不够稳定。
2.正态分布法。正态分布法运用正态曲线下面积与μ±μασ的关系来估计数值范围的。在图5.2中曾提到μ±1.96σ的范围内包含了曲线下总面积的95%,亦就是总例数的95%。在此范围外则有2.5%的例数其数据值大于μ±1.96σ,另2.5%小于μ-1.96σ。因此,就可用μ±1.96σ来估计双侧95%的正常值范围。同理可用μ与相应的μασ 估计所需百分范围,μ可从附表2查得。但在实际中μ与σ常常是不知道的,只能用它们的估计值X与S
来代替。估计正常值范围时常用的百分范围与相应的X±us见表5.1。用正态分布法估
计正常值范围的公式为
X±uαs (5.4)
例5.3 测得西安市7岁男童102人坐高,X=66.72,S=2.08,试用正态分布法估计
双侧95%正常值范围。
查表5.1,百分范围95,正态分布法双侧,应求X±1.96S。
代入公式(5.4)
66.72±1.96×2.08=(62.6432,70.7968)
西安市7岁男童坐高的95%正常值范围为62.6~70.08公分。
此法适用于正态分布资料,样本均数和标准差比较稳定者,其优点是结果稳定,受两端尾部数据影响较小,也不受样本数据极差的限制,缺点是只适用于正态分布资料。医学上不少资料呈偏态分布,但计算较繁。
作者:MedSci
版权声明:
本网站所有注明“来源:梅斯医学”或“来源:MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明“来源:梅斯医学”。其它来源的文章系转载文章,本网所有转载文章系出于传递更多信息之目的,转载内容不代表本站立场。不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。
在此留言









#统计学#
73